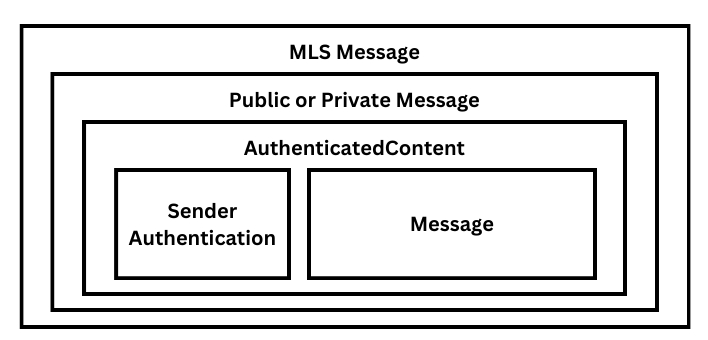
Solving A Problem
MLS in the context of other secure messaging protocols
-

The Signal Protocol
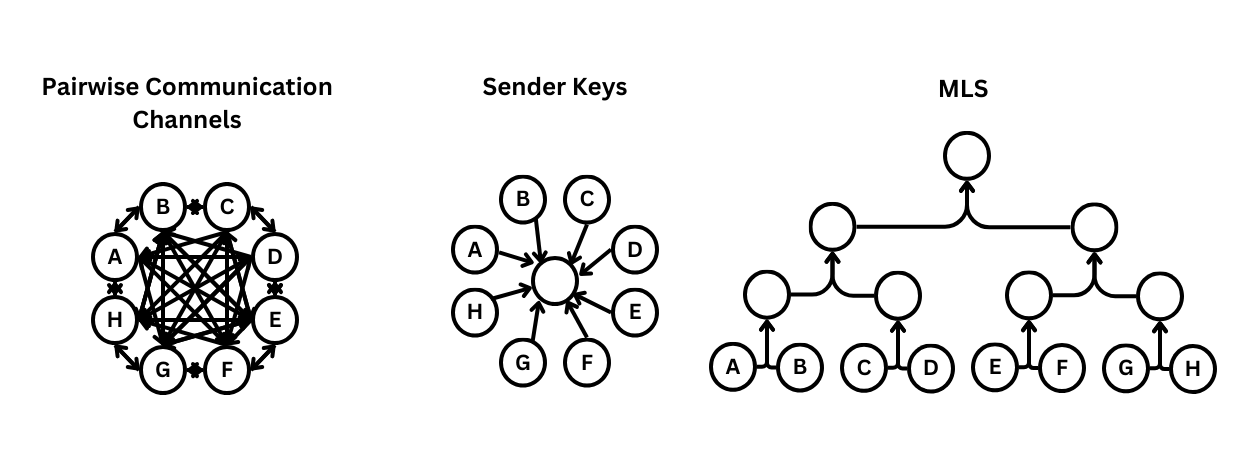
One of the most well-known secure messaging protocols to date, it has all of the required security properties, but only for communication between two parties. Extending this to group chats means creating pairwise communication channels between each member and every other member. This scales in O(n2)! It takes O(n) just to send a single message, since it has to be encrypted separately for everyone. Way too much work!
-

Sender Keys
Used by WhatsApp, the Sender Keys protocol involves a user sending the same symmetric key to all other group participants. (This assumes that secure two-way channels between individual members already exist or can be created temporarily.) Then sending messages is just O(1), encrypt once and let the server pass it on to all the other group members! And adding a new member is O(n), since the new member has to give their key to everyone else.
The bad news is that removing members is O(n2). All keys are deleted and the group essentially starts over, so that the leaving member doesn't have access to any of its secrets. Since everyone has to send their new key to everyone, this is quite inefficient.
Rotating a single member's key, in the case of compromise, is only O(n), but this is only weak post-compromise security, as an attacker is likely to have captured the entire user state, which includes the keys of the other users. It would be safer to do a full refresh, which is O(n2).
-

October 2018
Asynchronous Ratcheting Trees
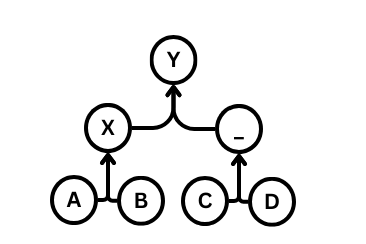
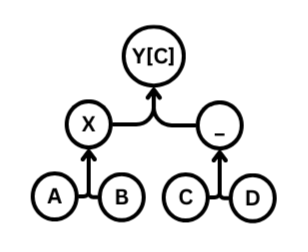
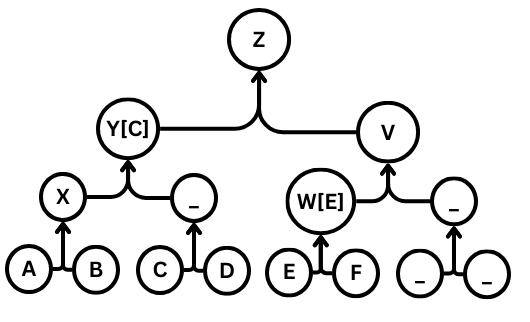
A paper from the ACM Conference on Computer and Communications Security which proposed an internal binary tree structure for efficient Diffie-Hellman key exchange within large groups. With O(1) message sending and O(lgn) key rotation and member removal, it formed the basis for a new protocol, MLS... which was codified as an Internet Standard in July 2023.
-

2023
Who uses MLS?
The secure messaging platform Wire boasts a full implementation of MLS, as one of the co-developers of the protocol itself. Google has also announced that it will be integrating MLS into Google Messages, giving this standard large industry backing.
-
So then
let's get to
the details!